Logistic Regression §

---

model setup §

Fitted Model:

• ->(= probability of the linear model True model of logistic regression:
• • π is the probability that an observation is in a specified category of the binary Y  variable, generally called the “success probability.”
    • The denominator of the model is (1 + numerator), so the answer will always be less than 1
    • The numerator must be positive, because it is a power of a positive value .

---

Model Estimation: §

==recall: OLSE in MLR, find to minimize== =>

• = observe

• -> estimate

• (look class notes 10.03)

---

Problems with binary §

1. error is also binary not normally distributed any more:
2. variance not constant ->OLS not optimal anymore
   • (from bernuli distribution)
3. Constraints on response variable:
   • ,
   • where linear function don’t keep this constraint

---

Model Estimation: §

Given :

that maximize where

---

Coefficient Interpretation §

Given:

Odds of success:

=>

1. For numerical predictor:
   • odds ratio of =
   • meeasure the changes in odds of success when increase by 1, the change is .
   • e.g:

= 1.0097 when age increases by 1, the odds of obese increases by 0.97%. case: if when , odds of success doesn’t change, is not related to

if when , odds of success increase by

if when , odds of success increase by

• see (class notes 10.05)

2. For categorical Predictors: Given:

is the reference

• when obs
• odds of success () =
• odds of success reference = when we choose , which other = 0, and all other predictors the same

= odds of success (D1)/odds of success reference, after complie the reference level, the odds of success in is different

example: (see class notes 10.05 page 10)

3. Tests in logistic Regression:
   • Wald test for individual coefficient
     • basically a t test in MLR
   • Deviane mel liklihood ratio test
     • alternative method for F test in MLR

---

Wald test for individual coefficient : V.S.

Test stats:

rejection rule: stat if is rejected, is a significant predictor of

---

Deviance likelihood Ratio Test:

F test compute the reduction in SSE () to check the significant improvnment in model.

rejection rule: if rejected, is significantly better than model

df =1

---

Model Diagnosis §

• Multicolinearity
  • stay the same for logistic regression(same as MLR)
• Influential points
• Not going to work:
  • MOdel Assumptions:
    • Heteroscedasticity
    • Nomality

---

Influential Points Detection

1. Pearson Residuals 2:

rule:

2. Deviance Residual

if :

if :

Rule : §

Confusion matrix:

---

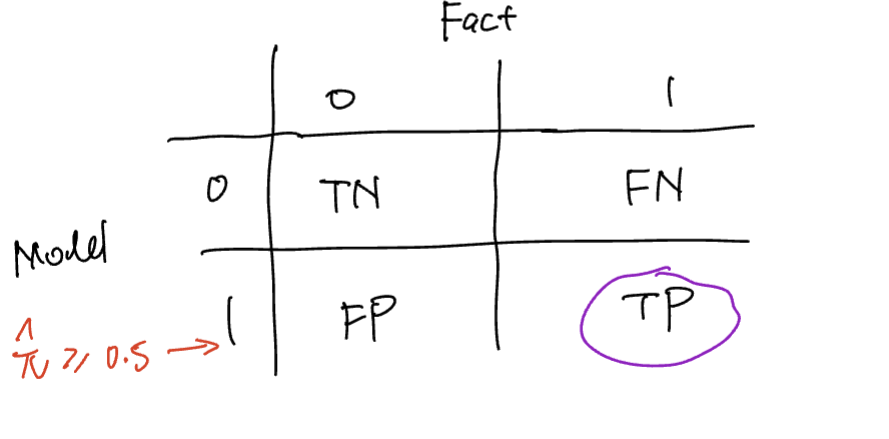
more Souce : https://online.stat.psu.edu/stat462/node/207/

TAGS §