Decomposition
Three major components for Time series :
- Trend component:
- Seasonal components:
- Remaining components(Noise):
Decomposition Method:
Classical Decomposition:
Classical Decomposition is the most common way steps:
- Decide the window size k for MA smoothing
- Assume that the seasonal component is constant, decide of the magnitude of the seasonal fluctuations is additive or multiplicative
- Additive: magnitude of the seasonal fluctuations around the trend does not change with time
- Multiplicative: magnitude of the seasonal fluctuations around the trend, is proportional to time , trend is increasing or decreasing, the magnitude of the seasonal fluctuations with trend
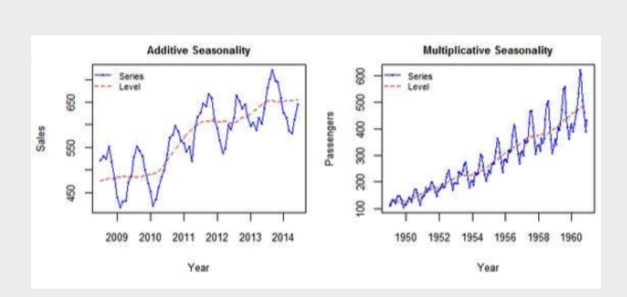
Additive Decomposition:
steps:
- Compute the trend component: Tt = wt from MA smoothing
- Compute the detrended data :
= − - To estimate the seasonal component for each season, simply average the detrended value for that season
- Remaining component (Noise):
= − −
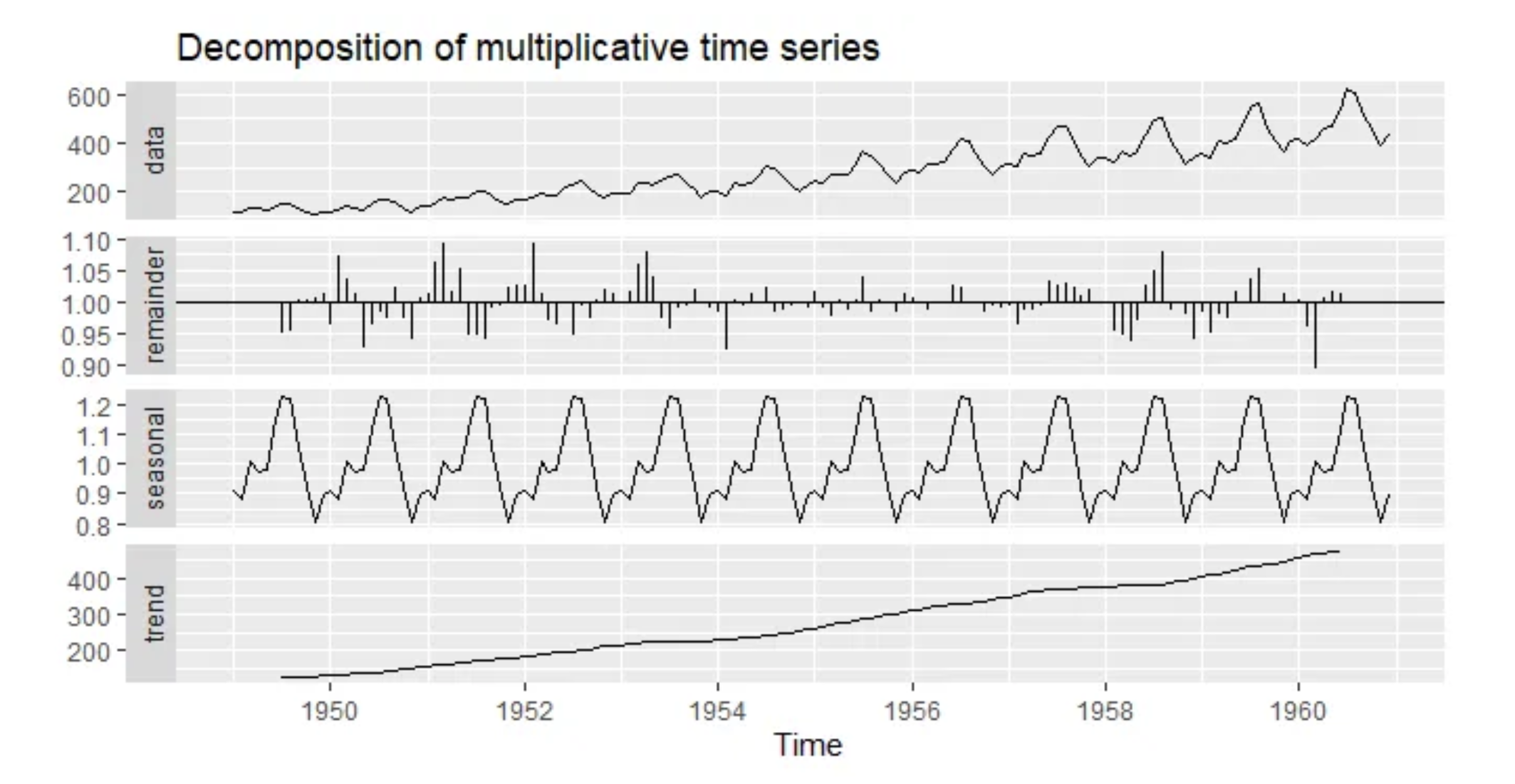
Multiplicative decomposition
steps:
- Compute the trend component: Tt = wt from MA smoothing
- Compute the detrended data :
= / - to estimate the seasonal component for each season, simply average the detrended values for that season. For example, with daily data, the seasonal component for each day of the week is the average of all the detrended values from the
same day of the week in the data
- Remaining component (Noise):
= 
Alternative Decomposition Methods
X11: based off classical decomposition with a fix of some
problems (only works for quarterly and monthly data);
SEATS: seasonal extracted by ARIMA model (only works for
quarterly and monthly data)
STL: Seasonal and Trend decomposition using Loess:
▶ The seasonal component is allowed to change over time, and
the rate of change can be controlled by the user.
▶ The smoothness of the trend-cycle can also be controlled by
the user.
▶ It can be robust to outliers (i.e., the user can specify a robust
decomposition), so that occasional unusual observations will
not affect the estimates of the trend-cycle and seasonal
components. They will, however, affect the remainder
component.
Disadvantage of Classical Decomposition
- The estimate of the trend-cycle is unavailable for the first few and last few observation( will base on the window function and does it set as center or rolling )
- the trend cycle estimate tends to over-smooth rapid rises and falls in the data
- it assume the seasonal component repeats for the same season( think of how we estimate
) - Classical decomposition methods assume that the seasonal component repeats from year to year.
- Occasionally, the values of the time series in a small number of periods may be particularly unusual. For example, the monthly air passenger traffic may be affected by an industrial dispute, making the traffic during the dispute different from usual. The classical method is not robust to these kinds of unusual values.